800＋名校学姐学长汇集于此，用自身申请经验解答你关于留学的任何疑问。

https://www.zhishiq.com/s/5f9f962d0ae96

首先，解答什么是卡方分布就需要了解这个分布为什么叫“卡方”。卡方，是音译自希腊字符 。卡方分布是由Karl Pearson在1900年提出的。

接着，我们应该去了解一下它的定义。维基百科上给出的定义如下：

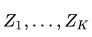
是独立、标准正态分布的随机变量，把他们的平方和计为Q。

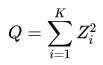
这个Q是服从自由度为K的卡方分布的。通常，也会被计为： 

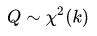
或者  

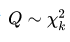
卡方分布只有一个变量，就是k。k在这里要求是正整数，它代表了自由度。

之后，我又参考了本科统计系的“圣经”，浙江大学第四版的《概率论与数理统计》中对于卡方分布的定义：

设

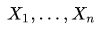
是来自总体N（0，1）的样本，则称统计量

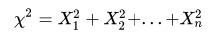
服从自由度为n的卡方分布，计为

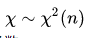
自由度是指上述等式中包含的独立变量的个数。书中还贴心的给出了分布的密度函数：

其中，

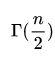
是伽马分布函数。

嗯，上面的定义都有一些抽象，下面，统计小菜鸡准备用R语言，给大家用图片的形式，直观地去看看这个“传说中”的卡方分布到底是长什么样子的。

首先，根据上面的定义，我们来验证一下

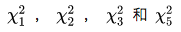
的形状。因为这个只是取了有限个的样本（1000000），所以，只能说近似泊松分布。

R语言的代码我贴在了下面：

x1 = rnorm(1000000)

x2 = rnorm(1000000)

x3 = rnorm(1000000)

x4 = rnorm(1000000)

x5 = rnorm(1000000)

Q1 = x1^2

Q2 = x1^2 + x2^2

Q3 = x1^2 + x2^2 + x3^2

Q5 = x1^2 + x2^2 + x3^2 + x4^2 + x5^2

par(mfrow=c(1,1))

plot(density(Q1), xlim = c(0,6), ylim = c(0,0.6), col = ‘blue’, lwd = 1.5, main = ‘chi-square’, xlab = ”, ylab=”)

lines(density(Q2), col = ‘black’, lwd = 1.5)

lines(density(Q3), col=’red’, lwd = 1.5)

lines(density(Q5), col=’green’, lwd = 1.5)

legend(‘topright’,c(‘df=1′,’df=2′,’df=3′,’df=5’),fill=c(‘blue’,’black’,’red’,’green’))

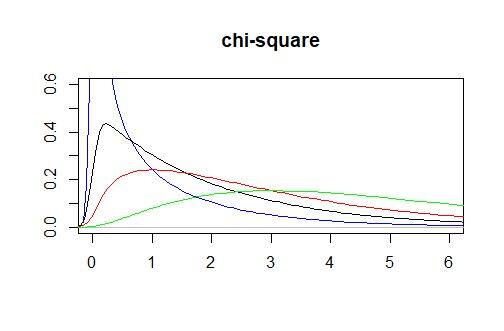
接着我采用了1000个样本量，为大家用R语言的内嵌卡方分布函数呈现了五个卡方分布的样子，分别是

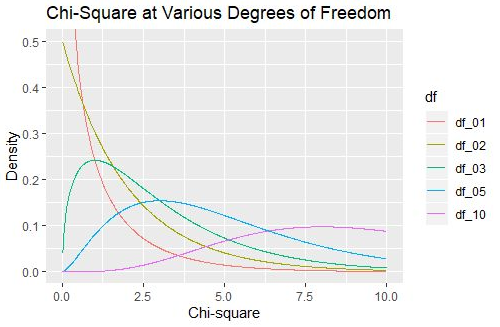
可以看出，泊松分布不像正态分布，它并没有对称这一特征，而且根据自由度的不同，长相也很“随意”。

得到这幅图的代码如下：

library(dplyr)

library(ggplot2)

library(tidyr)

data.frame(chisq = 0:1000 / 100) %>%

mutate(df_01 = dchisq(x = chisq, df = 1),

df_02 = dchisq(x = chisq, df = 2),

df_03 = dchisq(x = chisq, df = 3),

df_05 = dchisq(x = chisq, df = 5),

df_10 = dchisq(x = chisq, df = 10)) %>%

gather(key = “df”, value = “density”, -chisq) %>%

ggplot() +

geom_line(aes(x = chisq, y = density, color = df)) +

labs(title = “Chi-Square at Various Degrees of Freedom”,

x = “Chi-square”,

y = “Density”) +

coord_cartesian(ylim = c(0, 0.5))

在写这个问题的时候，看到了@普通人在“卡方分布怎么理解？”的回答，他的回答很有趣，用掷色子的例子非常形象的讲述了泊松分布是怎么诞生的，但是可能后面的simulation（拟合）部分有些深奥，如果有会python的同学看了真的会受益匪浅。

了解完了定义接着就是泊松分布的性质，浙大的《概率论和数理统计》书上主要讲了泊松分布的三个性质。

（1）、可加性（如果两个卡方分布相互独立，则它们相加的分布是两者自由度之和的泊松分布）

（2）、告诉了我们泊松分布的自由度和方差

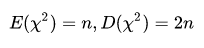
（3）、分布位点

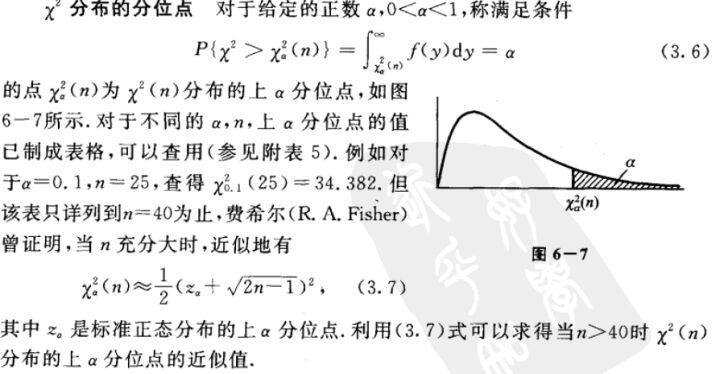
不仅如此，卡方分布还是t分布和F分布定义的重要组成部分，而t和F分布在方差检验和回归分析中又占有重要的地位。

除了上述性质以外，在George和Roger在statistical inference（统计推断）这本书里还提到，卡方分布也是指数分布簇的一员。关于卡方分布簇，统计推断这本书里有着一下的定义：

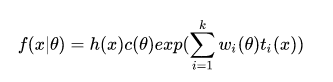
如果一个分布的密度函数能拆分成上述形式，则其属于指数分布簇。

这里我们变形一下，把泊松分布的密度函数变个形式：

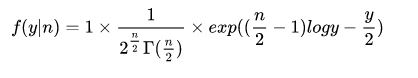
很容易看出基本符合上述指数族分布模型。为什么在这里要提指数分布族呢？

因为指数分布族中的分布以及指数分布族的性质具有族群性，就是说这几个分布之间是具有统一的规律和特性的。除此之外，指数分布族还具有很多优良的性质，这些性质在贝叶斯统计中也是非常重要的性质。指数分布族在机器学习(machine learning)模型的参数假设以及参数推理中有很广泛的运用。

如果要说卡方分布最广泛的应用在何处，我们就不得不提卡方检验。卡方检验归属于非参数检验部分，主要应用于比较两个及两个以上样本率(构成比）以及两个分类变量的关联性分析这两方面。

卡方检验在分类资料统计推断中的应用，包括：两个率或两个构成比比较的卡方检验；多个率或多个构成比比较的卡方检验以及分类资料的相关分析等。

芝士圈留学用户专属福利：

包含

推荐信（recommendation letter/RL）、个人陈述（personal statement/PS）

简历（Resume/CV）、动机函(SOP)、小essays

全部由名校外籍老师修改润色，质量很高

参考链接：https://www.zhishiq.com/s/5f9b834fcca68

新用户现在注册芝士圈留学，就能免费解锁一次学长学姐的申请档案

轻松查看世界名校申请过来人的

三围标化成绩、留学申请文书、实习科研经历等~

现在去解锁：https://www.zhishiq.com/s/5f9fada4398bd

邀请好友注册消费，好友得3张大额优惠券

（优惠覆盖文书修改、留学咨询等8类服务）

你也可获得好友消费金额的5%，可现金提现

现在去邀请：https://www.zhishiq.com/s/5ffe91a3addc3

跟着国内外大厂名企项目leader做项目，你将收获：

快速丰富项目实战经验，不断积累行业人脉

高含金量的推荐人推荐信

对接下来找工作或留学申请都极具竞争力！

查看更多实习项目：https://www.zhishiq.com/s/5ffe9849ad009

如需了解岗位详情，请登录芝士圈留学官网，添加你的专属客服咨询。

(登录成功后会即时弹出专属客服vx)

跟着顶尖院校大牛导师做科研，你将收获：

一段独一无二的科研经历

高含金量的推荐人推荐信

高水平国际英文会议论文发表

快速提升背景，冲刺藤校G5之路更顺畅！

查看更多科研项目：https://www.zhishiq.com/s/5ffe961eeda26

如需了解项目详情，请登录芝士圈留学官网，添加你的专属客服咨询。

(登录成功后会即时弹出专属客服vx)。

最新备考资料，持续更新

查看更多备考资料：https://www.zhishiq.com/s/5ffe9b49f1a54

如需更多备考干货，请登录芝士圈留学官网，添加你的专属客服咨询。

(登录成功后会即时弹出专属客服vx)